Smith-Waterman-Algorithm

概念

Smith-Waterman 算法是一种局部序列比对算法，用于在两个序列之间寻找最佳的局部相似区域。与 Needleman-Wunsch 算法类似，Smith-Waterman 算法也是基于动态规划的思想，但是它不允许负分数的出现 (负分替换为 0)，因此可以找到局部相似区域。

理解

要找到两个序列的最佳比对，也就是说要找到一条路径，使得路径上的得分最大。

为什么要用动态规划的思想：

比如我们要找到两个城市之间的最短距离，两个城市之间有若干个中间城市，如下图所示：

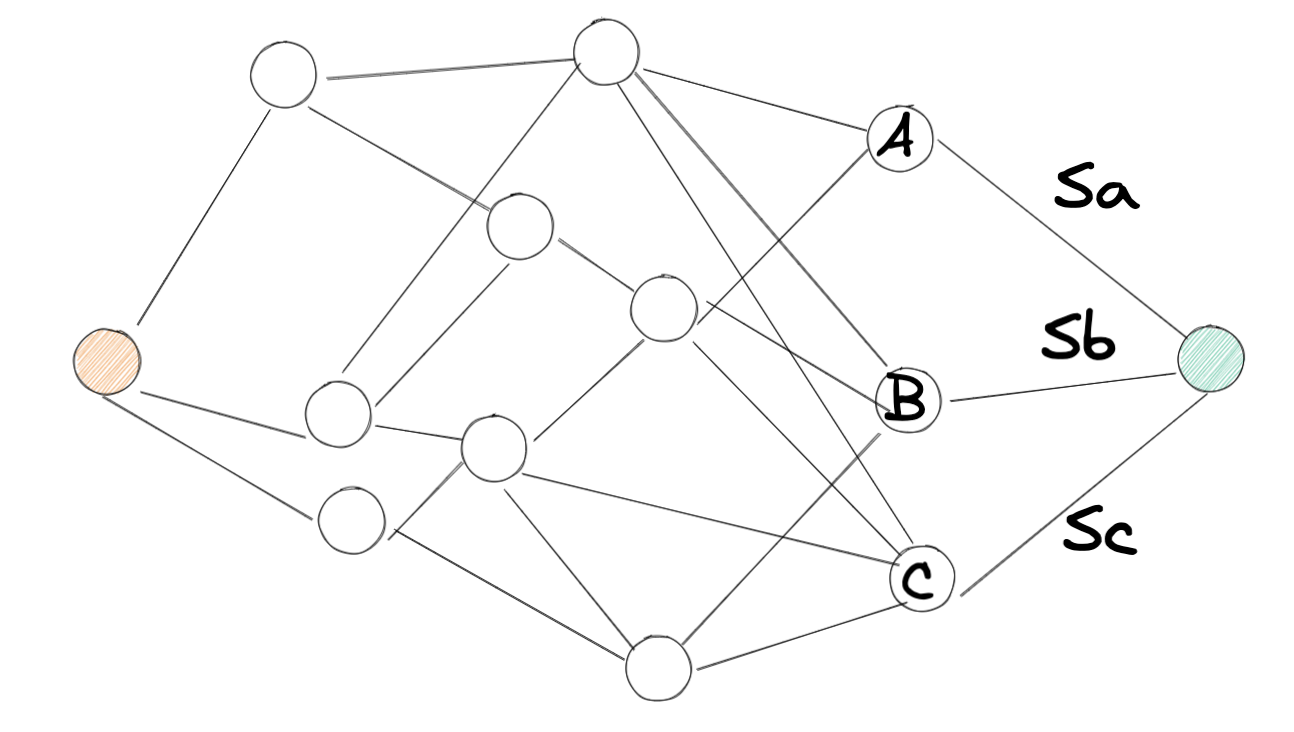
我们要找到红色点到橙色点的最短距离，可以把问题简化成红色点分别到 A,B,C 点的最短距离 (如果 Sa, Sb, Sc 相同的话), 以此往前类推，把问题分解成子问题，最后得到最优解。

步骤解释

1. 确定置换矩阵和空位罚分

置换矩阵

置换矩阵赋予每一碱基对匹配或错配的分数，相同或类似则赋予正值，不同或不相似赋予 0 分或者负分。

以核苷酸比对为例，若匹配 (match) 为 1 分，错配 (mismatch) 为 -1 分，则置换矩阵如下：

	A	T	C	G
A	1	-1	-1	-1
T	-1	1	-1	-1
C	-1	-1	1	-1
G	-1	-1	-1	1

也可以表示为：

$s(a_{i},b_{j})=\begin{cases}1,&a_{i}=b_{j}\\-1,&a_{i}\neq b_{j}\end{cases}$

氨基酸序列比对的置换矩阵一般更加复杂。通常性质相似的残基对具有正分数，反之，不相似的具有负分数。

空位罚分

空位罚分决定了引入或延长空位的分值。

空位罚分决定了插入或者删除的分值。最基本的空位罚分方式为每次插入或者删除的得分相同。

但是从生物学意义上来讲，插入或缺失相比碱基的错配，会带来更严重的影响，比如移码突变等，因此空位罚分一般会比错配分数更高。

另外，单个基因突变事件可能导致一长串空位的插入。因此，一个连续的较长的空位优于多个分散的小的空位。

虽然多个分散的小的空位可以产生更多匹配，但一个连续的较长的空位代表这个区域只在一个序列中出现，使用后者可以避免为了得到高分而过度匹配这段序列。

实现该方法只需要引入空位起始罚分和空位延长罚分的概念。空位起始罚分通常高于空位延长罚分。

空位权值恒定模型

该模型空位的罚分正比于空位的长度。

空位延伸罚分模型

$W_{k}=u(k-1)+v\quad (u>0,v>0)$

该模型考虑空位起始罚分和空位延长罚分，其中$v$为开始空位的罚分，$u$为每次延长空位的罚分。例如，一个长度为 2 的空位的罚分为$u+v$, 长度为 10 的空位的罚分为$9u+v$。

2. 初始化得分矩阵

得分矩阵的长度和宽度分别为两序列的长度 +1。其首行和首列所有元素均设为 0。

额外的首行和首列得以让一序列从另一序列的任意位置开始进行比对，分值为零使其不受罚分。

3. 计算得分矩阵

对得分矩阵的每一元素进行从左到右、从上到下的打分，考虑匹配或错配（对角线得分），引入空位（水平或垂直得分）分别带来的结果，取最高值作为该元素的分值。

如果分值低于 0，则该元素分值为 0。打分的同时记录下每一个分数的来源用来回溯。

举例：

给定两条序列 TGTTACGG 和 GGTTGACTA. 并使用如下置换矩阵和空位罚分：

• $s(a_{i},b_{j})=\begin{cases}1,&a_{i}=b_{j}\\-1,&a_{i}\neq b_{j}\end{cases}$

• $W_{k}=kW_{1}, W_{1} = 2$

初始化得分矩阵，然后进行打分，前三个碱基如下图所示：

其中黄色表示正在计算的两个碱基，黑色箭头和箭头上的分数表示分数来源和对应分数，得到矩阵上的值为计算不同来源得到的最大值。

比如第一对碱基，有三个方向：

• 上方的箭头为$0-2=-2$
• 左方的箭头为$0-2=-2$
• 左上角对角线的箭头为$0-3=-2$

这里最大的值为$-2$, 负数取$0$

再比如第三张小图，为G-G的碱基匹配对，也有三个方向：

• 上方的箭头为$0-2=-2$
• 左方的箭头为$0-2=-2$
• 左上角对角线的箭头为$0+3=3$

取最大值为$3$

tip

横向和竖向的箭头分数都是空位罚分，对角线的箭头分数是置换矩阵所得

最终以此理，我们可以得到如下的得分矩阵：

其中红色箭头代表分数的来源用于回溯，蓝色方块表示得分矩阵的最大值。

2. 回溯寻找最优比对

通过动态规划的方法，从得分矩阵的最大分值的元素开始回溯直至分数为 0 的元素。

具有局部最高相似性的片段在此过程中产生，如下图所示：

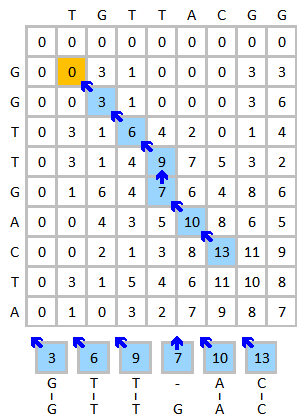
最终得到比对结果为：

G T T - A C
| | |   | |
G T T G A C

note

具有第二高相似性的片段可以通过从最高相似性回溯过程之外的最高分位置开始回溯，即完成首次回溯之后，从首次回溯区域之外的最高分元素开始回溯，以得到第二个局部相似片段。

代码实现

用 rust 写一个该算法的得分矩阵计算的基本实现：

// 1. define the score of match, mismatch and gap
const MATCH_SCORE: i64 = 3;
const MISMATCH_SCORE: i64 = -3;
const GAP_SCORE: i64 = -2;

fn smith_waterman(seq1: &str, seq2: &str) {

    // 2. initialize the matrix
    let mut matrix = vec![vec![0; seq2.len() + 1]; seq1.len() + 1];

    // 3. calculate the matrix
    for i in 1..=seq1.len() {
        for j in 1..=seq2.len() {
            // calculate the score from diagonal
            let diag_score = if seq1.chars().nth(i - 1) == seq2.chars().nth(j - 1) {
                MATCH_SCORE
            } else {
                MISMATCH_SCORE
            };

            // compare the three possible ways to get the current cell
            matrix[i][j] = std::cmp::max(
                matrix[i - 1][j - 1] + diag_score, // diagonal
                std::cmp::max(matrix[i - 1][j] + GAP_SCORE, matrix[i][j - 1] + GAP_SCORE), // left and up
            );

            // if matrix_score < 0, set it to 0
            matrix[i][j] = std::cmp::max(0, matrix[i][j]);
        }
    }
    // 4. display the matrix
    display_matrix(&matrix);
}

// pretty print the matrix
fn display_matrix(matrix: &Vec<Vec<i64>>) {
    for row in matrix {
        for cell in row {
            print!("{:4} ", cell);
        }
        println!();
    }
}

fn main() {
    let seq1 = "GGTTGACTA";
    let seq2 = "TGTTACGG";

    smith_waterman(seq1, seq2);
}

可以得到如下结果：

   0    0    0    0    0    0    0    0    0
   0    0    3    1    0    0    0    3    3
   0    0    3    1    0    0    0    3    6
   0    3    1    6    4    2    0    1    4
   0    3    1    4    9    7    5    3    2
   0    1    6    4    7    6    4    8    6
   0    0    4    3    5   10    8    6    5
   0    0    2    1    3    8   13   11    9
   0    3    1    5    4    6   11   10    8
   0    1    0    3    2    7    9    8    7

和我们推理得到的一致。

参考

• 
  维基百科