Part of series:Algorithm
时间复杂度
概念
时间复杂度分析不是统计算法的运行时间,而是运行时间随着数据规模增大的增长趋势。
举例:
// 算法 A 的时间复杂度:常数阶
fn algorithm_A(n: i32) {
println!("{}", 0);
}
// 算法 B 的时间复杂度:线性阶
fn algorithm_B(n: i32) {
for _ in 0..n {
println!("{}", 0);
}
}
// 算法 C 的时间复杂度:常数阶
fn algorithm_C(n: i32) {
for _ in 0..1000000 {
println!("{}", 0);
}
}- 算法 A: 只有打印操作,不管输入的 n 是多少,都只执行一次打印操作,所以时间复杂度是常数阶
- 算法 B: 打印操作的次数和 n 成正比,所以时间复杂度是线性阶
- 算法 C: 无论输入的 n 是多少,打印操作都是固定的 1000000 次,所以时间复杂度仍是常数阶
函数的渐进上界
给定一个函数,其接受参数的输入大小为 n:
fn algo(n: i32) {
let mut a = 1; // +1
a = a + 1; // +1
a = a * 2; // +1
// 循环 n 次
for _ in 0..n { // +1(每轮都执行 i ++)
println!("{}", 0); // +1
}
}该函数记为 ,其中 为常数项, 为线性项。
我们将线性阶的时间复杂度记为,这个数学符号称为大记号,表示函数的渐近上界(asymptotic upper bound)。
:::tip 渐进上界
计算渐近上界就是寻找一个函数 ,使得当趋向于无穷大时,和 处于相同的增长级别,仅相差一个常数项的倍数。
:::
推算方法
定义太过拗口,直接看推算方法。
1. 统计操作数量
针对代码,从上而下:
- 忽略常数项,因为对时间复杂度不产生影响
- 省略系数,例如循环 次和 次,都简化记为次
- 循环的嵌套用乘法
例如:
fn algo(n: i32) {
let mut a = 1; // +0(技巧 1)
a = a + n; // +0(技巧 1)
// +n(技巧 2)
for i in 0..(5 * n + 1) {
println!("{}", 0);
}
// +n*n(技巧 3)
for i in 0..(2 * n) {
for j in 0..(n + 1) {
println!("{}", 0);
}
}
}得到:
2. 判断渐进上限
时间复杂度是由最高阶的项决定的, 其他项可以忽略。
一些例子:
| 函数 | 时间复杂度 |
|---|---|
常见类型
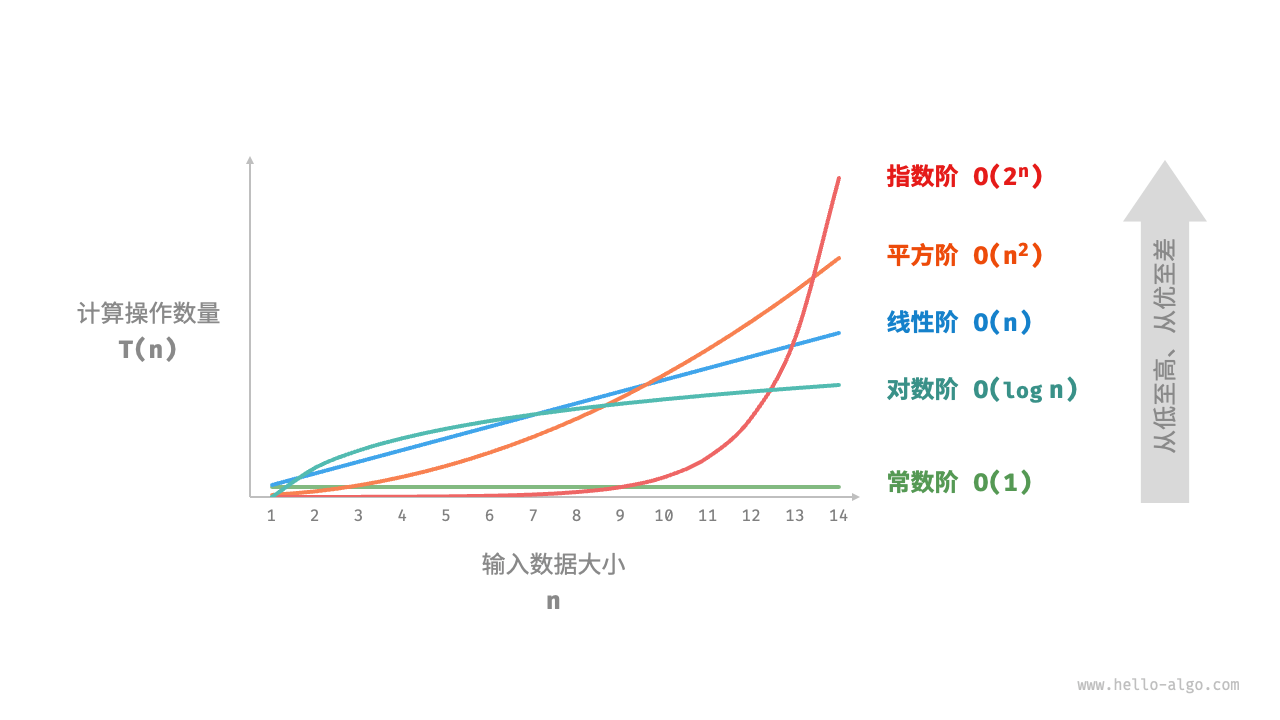
常见的时间复杂度类型可以按如下排序:
常数阶 < 对数阶 < 线性阶 < 线性对数阶 < 平方阶 < 指数阶 < 阶乘阶
1. 常数阶
/* 常数阶 */
fn constant(n: i32) -> i32 {
_ = n;
let mut count = 0;
let size = 100_000;
for _ in 0..size {
count += 1;
}
count
}2. 线性阶
/* 线性阶 */
fn linear(n: i32) -> i32 {
let mut count = 0;
for _ in 0..n {
count += 1;
}
count
}3. 平方阶
/* 平方阶 */
fn quadratic(n: i32) -> i32 {
let mut count = 0;
// 循环次数与数据大小 n 成平方关系
for _ in 0..n {
for _ in 0..n {
count += 1;
}
}
count
}4. 指数阶
有点像细胞分裂的例子,每次分裂都会产生两倍的细胞。
/* 指数阶(循环实现) */
fn exponential(n: i32) -> i32 {
let mut count = 0;
let mut base = 1;
// 细胞每轮一分为二,形成数列 1, 2, 4, 8, ..., 2^(n-1)
for _ in 0..n {
for _ in 0..base {
count += 1
}
base *= 2;
}
// count = 1 + 2 + 4 + 8 + .. + 2^(n-1) = 2^n - 1
count
}计算操作的总数为:
5. 对数阶
与指数阶相反,对数阶反映了“每轮缩减到一半”的情况。设输入数据大小为 ,由于每轮缩减到一半,因此循环次数是 .
/* 对数阶(循环实现) */
fn logarithmic(mut n: i32) -> i32 {
let mut count = 0;
while n > 1 {
n = n / 2;
count += 1;
}
count
}